Here at Portage Communications, we know that call center workforce management software must be both effective and affordable. Join our community for call center software with maximum productivity.

Our AgentTime™ software is a proven solution for your call center scheduling problems. We provide a one-time purchase with free customer support — forever.
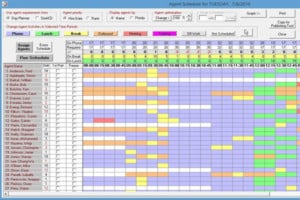
- Easily create weekly agent employee schedules with our smart AgentTime call center workforce management software.
- $1800.00. Advanced staffing tools start at just $60.00.
- Analyze the effects of service level goals, hold times, agent efficiency, and "what if" situations.
- Check out our demos, downloads, and our free fast staffing calculator.
Agent Time Scheduler
AgentTime™ Scheduler is the leading affordable call center workforce management software solution for small and medium-sized call centers. AgentTime creates schedules from your shift definitions, agent profiles, and agent requirements for inbound and outbound environments. It includes our Call Center Designer and SimACD. $1800.00 No monthly or set-up fees. Free support.
Sim ACD
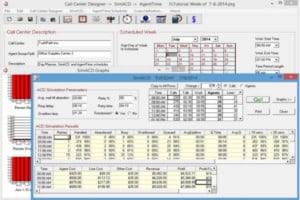
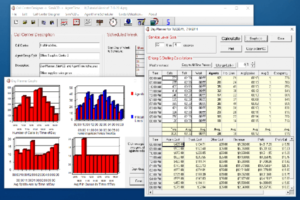
SimACD™ is a unique and precise approach to predicting the agent levels you need for call center scheduling. It’s a big step forward from existing staffing formulas. Using simulation, test and try out different agent staffing scenarios before implementing them in your call center. Observe caller abandonment behavior, queue times, service levels, and more in a computer-simulated automatic call distributor (ACD). Avoid costly staffing mistakes. $120.00
Call Center Designer
Call Center Designer™ is the best Erlang-C based staffing, prediction, modeling, and analysis solution for your call center. By time period, day, and week, Call Center Designer is your valuable and simple tool for solving the unique problems of staffing and managing small to medium-sized inbound call centers. $60.00





You have a GREAT product, it's a pleasure doing business with your company.
Rocco Pesolo, Abbot Laboratories